A tutorial on Opycleid

We give here a quick tutorial on the major features of Opycleid. Please consult the reference manual for a detailed description of the classes and methods.

Using existing category actions

In simple cases, one would just like to analyze chords, notes, etc. using the groups and monoids commonly used in transformational music theory, such as the transposition/inversion group, also known as the $T\text{/}I$ group, or the neo-Riemannian $\text{PRL}$ group.

Opycleid provides ready-to-use groups and monoids to perform such analysis. Let's take a famous example, first introduced by Richard Cohn (Richard Cohn: Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions, Music Analysis, 15(1), pp. 9-40, (1996).), namely the second movement of Beethoven's Ninth Symphony at bar 143. This is a progression of 19 major and minor triads, starting with C major, A minor, F major, D minor, B flat major, etc.

We would like to analyze this progression using the $\text{PRL}$ group. First, we create a new instance of opycleid.musicmonoids.PRL_Group.

from opycleid.musicmonoids import PRL_Group

my_group = PRL_Group()

The class opycleid.musicmonoids.PRL_Group inherits from opycleid.categoryaction.MonoidAction, which itself inherits from opycleid.categoryaction.CategoryAction. This latter class is the basis for all category actions, and provides three methods, mult, apply_operation, and get_operation for respectively composing musical transformations, applying a musical transformation to a musical element, and getting the possible transformations between two musical elements. In our case, we would like to determine which operation from the $\text{PRL}$ group takes C major to A minor, A minor to F major, F major to D minor, and so on. This is achieved in one line in Python by calling the method get_operation.

print(my_group.get_operation("C_M","A_m")) ## prints ['R']
print(my_group.get_operation("A_m","F_M")) ## prints ['L]
print(my_group.get_operation("F_M","D_m")) ## prints ['R']
print(my_group.get_operation("D_m","Bb_M")) ## prints ['L']

We see here that the Beethoven progression is built on a $R-L$ cycle.

To compare, we could analyze the same progression using the $T\text{/}I$ group, which is also implemented in Opycleid.

from opycleid.musicmonoids import TI_Group_Triads

my_group = TI_Group_Triads()

print(my_group.get_operation("C_M","A_m")) ## prints ['I4']
print(my_group.get_operation("A_m","F_M")) ## prints ['I9']
print(my_group.get_operation("F_M","D_m")) ## prints ['I2']
print(my_group.get_operation("D_m","Bb_M")) ## prints ['I7']

Coming back to the $\text{PRL}$ group, we could wonder what would yield the transformation $R$ applied to the G minor triad. This is achieved by calling the method apply_operation.

from opycleid.musicmonoids import PRL_Group

my_group = PRL_Group()
print(my_group.apply_operation("R","G_m")) ## prints ['Bb_M']

Finally, we can multiply operations by calling mult.

from opycleid.musicmonoids import PRL_Group

my_group = PRL_Group()
print(my_group.mult("RPL","R")) ## prints 'LP'

note: depending on your configuration, the names of the operations in the monoid might be different, although they represent the same transformation.

Defining custom morphisms and category actions

If the ready-to-use monoids and groups provided by Opycleid are not enough, it is possible to create one's own category action for specific musical purposes. In this section, we will see how to build morphisms and generate a category from them.

In our example use case, we would like to study major and augmented triads, and transformations between them. Instead of considering all triads in a single set, we are going to consider two distinct sets: one with the 12 major triads, which we denote by $X=\{C_M, C\sharp_M, D_M, E\flat_M, E_M, F_M, F\sharp_M, G_M, G\sharp_M, A_M, B\flat_M, B_M\}$ , and one with the 4 augmented triads, which we denote by $Y=\{C_{\text{aug}}, F_{\text{aug}}, D_{\text{aug}}, G_{\text{aug}}\}$ .

First, we need to define these category objects in Opycleid, by instantiating the class opycleid.categoryaction.CatObject

from opycleid.categoryaction import CatObject

X = CatObject("X",["C_M","Cs_M","D_M","Eb_M","E_M",
                   "F_M","Fs_M","G_M","Gs_M","A_M",
                   "Bb_M","B_M"])
Y = CatObject("Y",["C_aug","F_aug","D_aug","G_aug"])

Caution: all elements should have distinct names.

Then, we are going to define some morphisms of interest. The first one is simply the transposition operator acting on the set of the 12 major triads, which send $C$ major to $C\sharp$ major, $C\sharp$ major to $D$ major, and so on. In Opycleid, we need to instantiate the class opycleid.categoryaction.CatMorphism and define the action of this morphism on its domain.

from opycleid.categoryaction import CatMorphism

## We create a category morphism with name "T", domain X, and codomain X
T = CatMorphism("T",X,X)
T.set_mapping({"C_M":["Cs_M"],"Cs_M":["D_M"],"D_M":["Eb_M"],"Eb_M":["E_M"],
               "E_M":["F_M"],"F_M":["Fs_M"],"Fs_M":["G_M"],"G_M":["Gs_M"],
               "Gs_M":["A_M"],"A_M":["Bb_M"],"Bb_M":["B_M"],"B_M":["C_M"]})

Any instance of opycleid.categoryaction.CatMorphism is callable: one thus can get the action of a morphism on an element of its domain. For example, if we would like to know what is the image of $F$ major by the morphism $T$ , we would write the following.

print(T("F_M")) ## prints ['Fs_M']

Instances of opycleid.categoryaction.CatMorphism can be composed if their domain and codomain are compatible. For example, the composition of $T$ with itself gives, as expected, a transposition operator which moves the root of a major triad by two semitones.

T_2 = T*T
print(T_2("F_M")) ## prints ['G_M']

As we will see later, there is no need to explicitly calculate all possible compositions of morphisms. Instead, generators will be specified in a category, and Opycleid itself will generate the whole category.

Since we want to study transformations between major triads and augmented triads, we are going to define another morphism with domain $X$ and codomain $Y$ . Observe that, for any major triad, we get an augmented triad if the fifth is raised a semitone higher. This will define our second morphism, and we will call it f.

## We create a category morphism with name "f", domain X, and codomain Y
I = CatMorphism("f",X,Y)
I.set_mapping({"C_M":["C_aug"],"Cs_M":["F_aug"],"D_M":["D_aug"],"Eb_M":["G_aug"],
               "E_M":["C_aug"],"F_M":["F_aug"],"Fs_M":["D_aug"],"G_M":["G_aug"],
               "Gs_M":["C_aug"],"A_M":["F_aug"],"Bb_M":["D_aug"],"B_M":["G_aug"]})

Caution: all morphisms (and in particular, generators) in a category should have distinct names.

Conversely, if one lowers any note of an augmented triad by a semitone, one gets a major triad. Since, there are three possible notes, this defines a relation (and not simply a function) from $Y$ to $X$ . We will call this morphism g.

## We create a category morphism with name "g", domain Y, and codomain X
J = CatMorphism("g",Y,X)
J.set_mapping({"C_aug":["C_M","E_M","Gs_M"],
               "F_aug":["Cs_M","F_M","A_M"],
               "D_aug":["D_M","Fs_M","Bb_M"],
               "G_aug":["Eb_M","G_M","B_M"]})

We now create the category generated by the two objects $X$ and $Y$ , and the three morphisms $T$ , f, and g. For this, we instantiate opycleid.categoryaction.CategoryAction and specify the objects and the generators.

from opycleid.categoryaction import CategoryAction

my_category = CategoryAction()
my_category.set_objects([X,Y])
my_category.set_generators([T,I,J])
my_category.generate_category()
for name_f,f in my_category.get_morphisms():
  print(name_f)
'''
This prints the following list:
T
TT
TTT
TTTT
TTTTT
TTTTTT
TTTTTTT
TTTTTTTT
TTTTTTTTT
TTTTTTTTTT
TTTTTTTTTTT
TTTg
TTg
Tg
f
fT
fTT
fTTT
fTTTg
fTTg
fTg
g
gf
gfT
gfTT
gfTTT
id_X
id_Y
'''

This can also be done in one step during instantiation.

from opycleid.categoryaction import CategoryAction

my_category = CategoryAction(objects=[X,Y],generators=[T,I,J],generate=True)
for name_f,f in my_category.get_morphisms():
  print(name_f)

During the generation process, the names are obtained by concatenation. We can ask Opycleid to rewrite these operations.

my_category.rewrite_operations()
for name_f,f in my_category.get_morphisms():
  print(name_f)
'''
This prints the following list:
(T^10)
(T^11)
(T^2)
(T^2)g
(T^3)
(T^3)g
(T^4)
(T^5)
(T^6)
(T^7)
(T^8)
(T^9)
T
Tg
f
f(T^2)
f(T^2)g
f(T^3)
f(T^3)g
fT
fTg
g
gf
gf(T^2)
gf(T^3)
gfT
id_X
id_Y
'''

Note: the rewriting process of Opycleid is very basic, and only tries to identify repeated consecutive sequences of generators names.

Our category is such that

There are 16 morphisms from to :
- 12 of the form $T^p$ with $p=0\ldots11$ ( $T^0$ being $\text{id_X}$ ), and
- 4 of the form $(T^p)gf$ with $p=0\ldots3$ (here gf(T^3), gf(T^2), gfT, and gf, since $'(T^p)gf=gf(T^p)$ as can be verified directly in Opycleid).
There are 4 morphisms from to :
- of the form $f(T^p)g$ with $p=0\ldots3$ ( $fg$ being equal to $\text{id_Y}$ )
There are 4 morphisms from to :
- of the form $fT^p$ with $p=0\ldots3$
There are 4 morphisms from to :
- of the form $(T^p)g$ with $p=0\ldots3$

Now that our category is generated, we can use it for analyzing transformations between chords. For example, we could ask what are the transformations between $E$ major and $A$ major.

print(my_category.get_operation("E_M","A_M"))
## Prints ['(T^5)', 'gfT']

Indeed we can just transpose $E$ major by five semitone higher, using $T^{5}$ , or we can transform $E$ major to $C$ augmented using f, then to $G\sharp$ major by using g, and finally to $A$ major by using $T$ .

Defining monoid action morphisms

In the framework of Opycleid, an instance of opycleid.categoryaction.CategoryAction is a concrete implementation of a faithful functor $S \colon \mathbf{C} \to \mathbf{Rel}$ , where $\mathbf{C}$ is a small category, and $\mathbf{Rel}$ is the 2-category of finite sets and relations. Such a functor defines a "context" for the analysis: in the example above, we worked in the set of the major and minor triads, or in the two distinct sets of major triads and augmented triads.

It is naturally to ask whether an analysis context can be changed. This is the role of category action morphisms. By definition, a morphism between two category actions $S \colon \mathbf{C} \to \mathbf{Rel}$ and $S' \colon \mathbf{C'} \to \mathbf{Rel}$ is a pair $(N,\nu)$ where

$N$ is a functor from $\mathbf{C}$ to $\mathbf{C'}$ , and
$\nu$ is a lax natural transformation from $S$ to $S'N$ , i.e. for any morphism $f \colon X \to Y$ in $\mathbf{C}$ , the relation $\nu_Y \circ S(f)$ is included in the relation $S'N(f) \circ \nu_X$ .

Opycleid provides two classes, opycleid.categoryaction.CategoryFunctor and opycleid.categoryaction.CategoryActionFunctor, which define the functor $N \colon \mathbf{C} \to \mathbf{C'}$ , and the category action morphism $(N,\nu)$ respectively.

To illustrate the notion, consider the $T\text{/}I$ group introduced previously. This is an extension $1 \to \mathbb{Z}_{12} \to T\text{/}I \to \mathbb{Z}_{2} \to 1$ , where the homomorphism $\pi \colon T\text{/}I \to \mathbb{Z}_{2}$ sends the transposition operations $T^p$ to the identity of $\mathbb{Z}_{2}$ , whereas the inversion operations $I^p$ are sent to the non-trivial element of $\mathbb{Z}_{2}$ . The group $\mathbb{Z}_{2}$ can be made to act on the set of $\{major,minor\}$ of chord types in an obvious manner. We can are then going to build a category action morphism between these two category actions.

First, we define the group $\mathbb{Z}_{2}$ and its action.

from opycleid.categoryaction import CatObject, CatMorphism, MonoidAction

S = CatObject("S",["major","minor"])

Z = CatMorphism("z",S,S)
Z.set_mapping({"major":["minor"],"minor":["major"]})

Z2_group = MonoidAction()
Z2_group.set_objects([S])
Z2_group.set_generators([Z])
Z2_group.generate_category()

We also need to instantiate the $T\text{/}I$ group.

from opycleid.musicmonoids import TI_Group_Triads

G = TI_Group_Triads()

To define the category action morphism, we need first to define the functor $N$ from the $T\text{/}I$ group to the $\mathbb{Z}_{2}$ group. This is easily done by specifying the images of the generators of the $T\text{/}I$ group.

from opycleid.categoryaction import CategoryFunctor

generator_mapping={"T1":"id_S","I0":"z"}

N=CategoryFunctor(G,Z2_group)
N.set_from_generator_mapping(generator_mapping)
print(N.is_valid())
## Prints True

We then define the category action morphism. Since both the source and target category actions are in fact monoid actions, the natural transformation $\nu$ has only one component for the single object of the $T\text{/}I$ group. This component maps any chord to its type (major/minor).

elements = G.get_object()[1].get_elements()
element_mapping = {}
for x in elements:
    if x[-1]=="M":
        element_mapping[x]=["major"]
    else:
        element_mapping[x]=["minor"]

## This is the (only) component of the natural transformation    
eta = CatMorphism("eta",G.get_object()[1],Z2_group.get_object()[1])
eta.set_mapping(element_mapping)

Finally we instantiate a opycleid.categoryaction.CategoryActionFunctor which defines the category action morphism between the $T\text{/}I$ group and the $\mathbb{Z}_{2}$ group.

from opycleid.categoryaction import CategoryActionFunctor

## We assemble everything in the final category action morphism
Neta = CategoryActionFunctor(G,Z2_group,N,{".":eta})

print(Neta.is_valid())
## Prints True

Category action morphisms are especially useful for network analysis, which is presented below.

Klumpenhouwer and poly-Klumpenhouwer network analysis

Opycleid provides the means to perform Klumpenhouwer network (K-Net) and poly-Klumpenhouwer network (PK-Net) analysis.

Informally, a K-Net is a directed graph, the vertices of which are labelled with musical objects, and the arrows of which are labelled with transformations between them. Arrows are understood to be composable: the label of a resulting composite arrow should be equal to the label of the composition of the two original arrows.

A K-Net allows one to study the interconnections between different musical elements, for example in the study of the different intervals in the constitutive elements of chords in post-tonal music.

Recent research (see Alexandre Popoff, Moreno Andreatta, Andrée Ehresmann: Relational poly-Klumpenhouwer networks for transformational and voice-leading analysis, Journal of Mathematics and Music, 12:1 (2018), pp. 35-55) has proposed to extend the traditional framework of Klumpenhouwer networks. The categorical formalizations of the K-Net notion, leads to the notion of poly-Klumpenhouwer network which corresponds to the data $(R,S,F,\phi)$ of

a lax functor $R \colon \Delta \to \mathbf{Rel}$ , called the diagram action,
a functor $S \colon \mathbf{C} \to \mathbf{Rel}$ where $\mathbf{C}$ is a finite category called the context action, and
a category action morphism $(F, \phi)$ between them, i.e. a functor $F \colon \Delta \to \mathbf{C}$ , and a lax natural transformation $\phi \colon R \to SF$ (left-total on all components).

The diagram category action represents the network itself. The context category action is, as its name indicates, the context for analysis, i.e. musical transformations and their action on musical elements. The role of the functor $F \colon \Delta \to \mathbf{C}$ is to label the arrows of the network in the diagram category action by morphisms (musical transformations) in the context category action , whereas the role of the natural transformation $\phi$ is to label the elements of the network with musical elements from the context.

A PK-Net is created in Opycleid by instantiating the class opycleid.knetanalysis.PKNet using a category action which will serve as the context. For example, let's study the Beethoven progression we have seen above, this time using the $T\text{/}I$ group acting on major and minor triads.

## G is the previously instantiated TI_Group_Triads (see above)

from opycleid.knetanalysis import PKNet

my_knet = PKNet(G)

As we will see later, Opycleid allows one to define complex networks by specifying edges and vertices. If one has a list of musical elements, Opycleid can also generate all the possible PK-Nets with a diagram category action in which

objects are singletons, corresponding to each musical element, and
there is only one morphism between pairs of objects corresponding to the musical transformation taking one element to another.

These PK-Nets can be obtained by calling the Python generator from_progression(list_elements), which takes a list of musical elements and yields all possible PK-Nets. Note that an exception will be raised if no transformation exists between musical elements.

In the case of the Beethoven progression, the $T\text{/}I$ group acts simply transitively on major and minor triads, so only one PK-Net can be obtained, as shown below.

beethoven_progression = ["C_M","A_m","F_M","D_m","Bb_M"]
for pknet in my_knet.from_progression(beethoven_progression):
    print(pknet)
'''
X_0 -- I4 --> X_1
[['C_M']] -> [['A_m']]
X_1 -- I9 --> X_2
[['A_m']] -> [['F_M']]
X_2 -- I2 --> X_3
[['F_M']] -> [['D_m']]
X_3 -- I7 --> X_4
[['D_m']] -> [['Bb_M']]
'''

The context of a PK-Net can be changed by using a category action morphism, which yields a new PK-Net in the new context category action. This is done by calling the method global_tansform(cat_action_functor), where cat_action_functor is an instance of opycleid.categoryaction.CategoryActionFunctor representing the category action morphism. For example, if we use the monoid action morphism between the $T\text{/}I$ group and the $\mathbb{Z}_{2}$ group we defined in the previous section, we get the following new PK-net.

pknet = list(my_knet.from_progression(beethoven_progression))[0]
new_pknet = pknet.global_transform(Neta)
print(new_pknet)
'''
X_0 -- z --> X_1
[['major']] -> [['minor']]
X_1 -- z --> X_2
[['minor']] -> [['major']]
X_2 -- z --> X_3
[['major']] -> [['minor']]
X_3 -- z --> X_4
[['minor']] -> [['major']]
'''

As expected, we have transformed our original PK-net describing chords and their transformations to a new PK-net describing chord types and their transformations.

A PK-Net can also be defined from scratch by specifying all the edges and vertices. For example, we would like to define the complex network of pitch classes and their transformations in the $T\text{/}I$ group (acting on pitch classes) which is shown below.

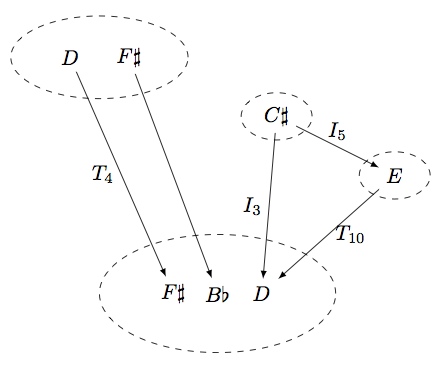
complexpknet

The following code defines the above PK-Net using Opycleid.

from opycleid.categoryaction import CatObject, CatMorphism
from opycleid.knetanalysis import PKNet
from opycleid.musicmonoids import TI_Group_PC
G = TI_Group_PC()

X = CatObject("X",["pX1","pX2"])
Y = CatObject("Y",["pY1"])
W = CatObject("W",["pW1","pW2","pW3"])
Z = CatObject("Z",["pZ1"])

f = CatMorphism("f",X,W)
f.set_mapping({"pX1":["pW1"],"pX2":["pW2"]})

g = CatMorphism("g",Y,W)
g.set_mapping({"pY1":["pW3"]})

h = CatMorphism("h",Y,Z)
h.set_mapping({"pY1":["pZ1"]})

k = CatMorphism("k",Z,W)
k.set_mapping({"pZ1":["pW3"]})

my_pknet = PKNet(G)
my_pknet.set_edges([f,g,h,k])
my_pknet.set_mappings({"f":"T4","g":"I3","h":"I5","k":"T10"},
                  {"pX1":["D"],"pX2":["Fs"],
                   "pY1":["Cs"],
                   "pW1":["Fs"],"pW2":["Bb"],"pW3":["D"],
                   "pZ1":["E"]
                  }
                 )
print(my_pknet)
'''
X -- T4 --> W
[['D'], ['Fs']] -> [['Fs'], ['Bb'], ['D']]
Y -- I3 --> W
[['Cs']] -> [['Fs'], ['Bb'], ['D']]
Y -- I5 --> Z
[['Cs']] -> [['E']]
Z -- T10 --> W
[['E']] -> [['Fs'], ['Bb'], ['D']]
'''

We define the four sets of the network $X$ , $Y$ , $W$ , and $Z$ as instances of opycleid.categoryaction.CatObject. Then we define the morphisms between these sets, i.e. the generating arrows/edges of our network, as instances of opycleid.categoryaction.CatMorphism. We then instantiate a new PK-Net with context category action the $T\text{/}I$ group acting on pitch classes, and we set the edges by calling the method set_edges with argument the list of opycleid.categoryaction.CatMorphism we just created. The diagram category action will then be created internally. Note that we do not need to explicitly specify the objects as they are automatically deduced from the morphisms. Finally, we define the mapping of edges and elements, by calling set_mappings with two arguments:

The first dictionary corresponds to the mapping of the generating edges, i.e. the image of the generating morphisms in the context category action.
The second dictionary corresponds to the mapping of the elements of the objects. The mappings must be left-total, i.e. each element must be related to at least one element in the context category action.

Opycleid will detect non-valid mappings and raise exceptions accordingly.